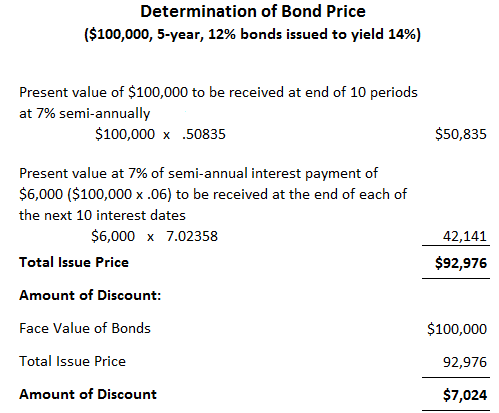
Bonds are issued at values other than face value (i.e. above or below their face value). If the prevailing market interest rate is above the stated rate, bonds will be issued at a discount. Conversely, if the prevailing interest rate is below the stated rate, bonds will be issued at a premium. To illustrate the issuance of bonds at a discount, suppose that on 2 January 2020, Valenzuela Corporation issues $100,000, 5-year, 12% term bonds. The interest of 6% is payable semi-annually on 2 January and 1 July. The bonds are issued when the prevailing market interest rate for such investments is 14%. Thus, the bonds are issued at a discount to yield 14%. This rate is also called the effective interest rate. Based on this effective rate, the bonds would be issued at a price of 92.976, or $92,976. The journal entry to record the Valenzuela bonds is shown as: As this entry illustrates, Cash is debited for the actual proceeds received, and Bonds Payable is credited for the face value of the bonds. The difference of $7,024 is debited to an account called Discount on Bonds Payable. The Discount on Bonds Payable account is a contra-liability account in that it is offset against the Bonds Payable account on the balance sheet in order to arrive at the bonds' net carrying value. To illustrate, a balance sheet prepared on 2 January 2020, immediately after the bonds were issued, would show the following under the long-term liability section: This section explains how to use present value techniques to determine bond prices. Given the prevailing market interest rate, the stated or coupon interest rate, and the maturity date, bond prices can be calculated using present value techniques. When bonds are issued, the borrower agrees to make two different types of payments: an annuity made up of the future cash interest payments and a single future amount constituting the bond's maturity value. Rational investors would not pay any more than the present value of these two future cash flows, discounted at the desired yield rate. The issue price of $92,976 is calculated in the table above. As the table shows, the issue price is composed of the present value of the maturity payment of $100,000 discounted at 7% for 10 periods, and the present value of semi-annual cash interest payments of $6,000 ($100,000 x .06), also discounted at 7%. The periods are used because the 5-year bonds pay interest semi-annually. The discount rate is the semi-annual yield or an effective rate of 7%. It is worth remembering that the $6,000 annuity, which is the cash interest payment, is calculated on the actual semi-annual coupon rate of 6%. Borrowers and investors need not make these calculations. Various bond tables are available that determine the correct prices at different yield rates and maturity dates. It is important to understand the nature of the Discount on Bonds Payable account. In effect, the discount should be thought of as an additional interest expense that should be amortized over the life of the bond. Remember that the bond was issued at a discount because the stated rate was below the market rate. Bondholders receive only $6,000 every 6 months, whereas comparable investments yielding 14% are paying $7,000 every 6 months ($100,000 x .07). The discount of $7,024 represents the present value of the $1,000 difference that the bondholders are not receiving over each of the next 10 interest periods (5 years' interest paid semi-annually). Essentially, the company incurs the additional interest, amounting to $7,024, at the time of issuance by receiving only $92,976 rather than $100,000. However, due to the matching concept, this cost of $7,024 cannot be expensed when the bonds are issued but must be written off over the life of the bond. As a result of issuing the bonds at a discount, the total interest expense incurred by Valenzuela Corporation over the 5-year life of the bond is $67,024, which is calculated as follows: Another way to view this is to examine the difference between the cash that the company will eventually repay to bondholders versus what it received at the time of issuance. This calculation is: The discount of $7,024 must be written off or amortized over the life of the bond. Two methods are available to do this: the straight-line method and the effective-interest method. The effective-interest method is conceptually preferable, and accounting pronouncements require its use unless there is no material difference in the periodic amortization between it and the straight-line method. However, the straight-line method is easy to apply and understand. For this reason, it is worth examining first in order to aid in your understanding of the core concepts.Accounting for Bonds Issued at a Discount

Using Present Value to Determine Bond Prices
Nature of the Discount Account


Amortizing the Discount
Accounting for Bonds Issued at a Discount FAQs
A bond that is issued at a discount is a bond that has been issued for less than the par value of the bond. The difference between the par value and the purchase price is referred to as the "discount."
Yes, there are risks associated with buying a bond at a discount. One risk is that the bond may not be redeemed at the par value when it matures. This could result in the investor losing money if they sell the bond at a price below the par value.
A bond issuer benefits from issuing a bond at a discount because they are able to raise money at a lower cost. This can be helpful if the issuer is looking to finance a large project.
If there was a discount on bonds payable, then the periodic entry is a debit to interest expense and a credit to discount on bonds payable; this has the effect of increasing the overall interest expense recorded by the issuer.
A basic rule of thumb suggests that investors should look to buy premium bonds when rates are low and discount bonds when rates are high. Because premium bonds typically provide higher coupon payments, the biggest risk is that they could be called before the stated maturity date.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













