Sum-of-the-years' digits is a method that uses an arbitrary arithmetic system to derive the annual depreciation charges. It is known as an accelerated depreciation method. In this method, you multiply the depreciable basis amount by an annual fraction. The denominator is the sum of the digits from 1 to n, where n is the number of years in the asset's service life. Depreciation is calculated under sum-of-the-years' digits by adding up the number of years in an asset's useful economic life. For example, if an asset has a 5-year economic useful life, the numbers 1, 2, 3, 4 and 5 are added, and the resulting sum (15) becomes the denominator while the numerator is the number of remaining years of the useful economic life of the asset. Accordingly, the depreciation to be provided for an asset with a 5-year life is: Depreciation determined in this way constitutes the annual depreciation expense, which is applied to the cost of acquisition or construction of the asset to be depreciated rather than the asset's written-down value. The advantages and disadvantages of this method are more or less the same as the declining balance method. The exception is that the calculations needed in sum-of-the-years' digits are slightly more complex. The formula to calculate depreciation expense using sum-of-the-years' digits is shown below. The sum-of-the-years' digits method is another variation on accelerated depreciation. Under this method, an asset's depreciable base is multiplied by a declining rate. Note that the asset's residual value is subtracted from its acquisition cost to determine its depreciable base. This rate is a fraction, in which the numerator is the number of years remaining in the asset's life at the beginning of the year and the denominator is the sum of the digits of the asset's useful life. To demonstrate how this fraction is worked out, suppose that an asset has a 5-year life. In the first year, the rate is a fraction that has a numerator of 5, the number of years remaining at the beginning of the year. In addition, the denominator of the fraction is 1 + 2 + 3 + 4 + 5 = 15. To take an example, in the second year, the fraction would be 4/15, and so on. The depreciation schedule using sum-of-the-years' digits for equipment is shown below. As with the double-declining-balance method, the sum-of-the-years' digits method allocates more depreciation in the early years and less in later years. However, unlike the double-declining balance method, the sum-of-the-years-digits method is calculated by applying a declining rate to a constant base: the asset's depreciable cost. Partial-year depreciation also can be calculated using the sum-of-the-years' digits method. For example, suppose that a company purchases equipment on 1 October of the current year. In this case, the equipment is in use for only 3 months during the year, and the sum-of-the-years' digits depreciation is $3,000, calculated as follows: $3,000 = 3/12 x $12,000, or 3/12 x ($36,000 x 5/15) In the second year, the depreciation expense of $11,400 must be calculated in two steps, as follows: 9/12 x ($36,000 x 5 / 15) = $9,000
3/12 x ($36,000 x 4/15) = $2,400
$9,000 + $2,400 = $11,400 Depreciation expense for the remaining three years is calculated in a similar way. Both the declining balance and sum-of-the-years' digits methods are examples of accelerated depreciation. From a conceptual perspective, these methods are most suited for assets that give up a greater portion of their benefits in their early years. As such, most of the cost of these assets should be allocated to these same early years. High-tech products are examples of assets in which the decline of benefits is likely to follow such a pattern. Accelerated depreciation is also appropriate for assets that have higher repair expenses in later years. This results in a reasonably constant expense related to the asset because depreciation expense declines as repair expense increases. Regardless of these conceptual arguments, a company's managers can choose between these accelerated depreciation methods for any depreciable asset. The only guideline is that the depreciation method should be systematic and rational, and as we noted, all of the depreciation methods discussed so far meet this requirement. Furthermore, management can choose straight-line depreciation for financial reporting purposes and a special form of accelerated depreciation for tax purposes. This allows a firm to report higher income for financial statement purposes and lower Income for tax return purposes: If an asset's useful service life is 5 years, the denominator is the total of each year's digits: namely, 1 + 2 + 3 + 4 + 5, which is 15. The formula to work out the denominator (D) is D = n(n+1) / 2. The numerator becomes smaller each year. It starts with the value n in the first year and decreases by 1 each year until it equals 1 in the final year of the asset's estimated service life. Therefore, the annual fractions for an asset with a 5-year life are (in order): 5/15, 4/15, 3/15, 2/15, and 1/15. The tables below show the application of the sum-of-the-years' digits approach to this asset.Sum-of-the-Years’ Digits: Definition
Sum-of-the-Years’ Digits: Explanation
Advantages and Disadvantages of Sum-of-the-Years’ Digits Method of Depreciation
Formula

The fraction's denominator can easily be calculated using the following formula:
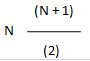
where N is the asset's useful economic life. For the above example, where the asset's life is 5 years, the denominator is calculated as follows:
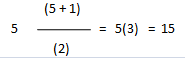
If the asset's life is 10 years, the denominator is:
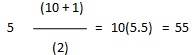

Example

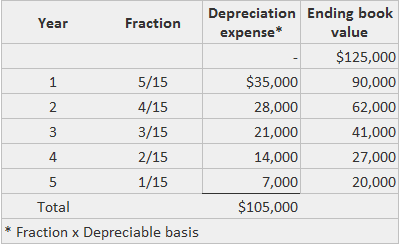
Sum of Years’ Digits Method of Assets Depreciation FAQs
According to the sum of years' digits method, the Depreciation expense is greater in earlier years (due to higher depreciable cost) and decreases over time until it becomes zero at the end of the asset's useful life. The straight-line Depreciation expense is the same each year, because there are no residual values involved.
The primary advantage of this method is that it provides a more accurate trend for Depreciation expenses. That is, the expense tends to be higher in early years, which makes sense if an asset gives up its benefits faster earlier on.
This approach requires a larger number of calculations and may be difficult for management to implement. However, the additional work is likely justified by the benefits of using more accurate numbers that provide a better match between Depreciation expense and revenue.
This approach requires straight-line Depreciation rates and an asset’s useful life (which is the time period over which it will be used/depreciated). It also assumes that an asset loses value evenly over time. Finally, this method requires management to determine the appropriate Depreciation rate.
The sum-of-years digits method of depreciating assets has the effect of increasing the value of net income because it discounts expenses over time. This has the effect of making profits higher than they would be if they were calculated using the more traditional approach of straight-line Depreciation.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













