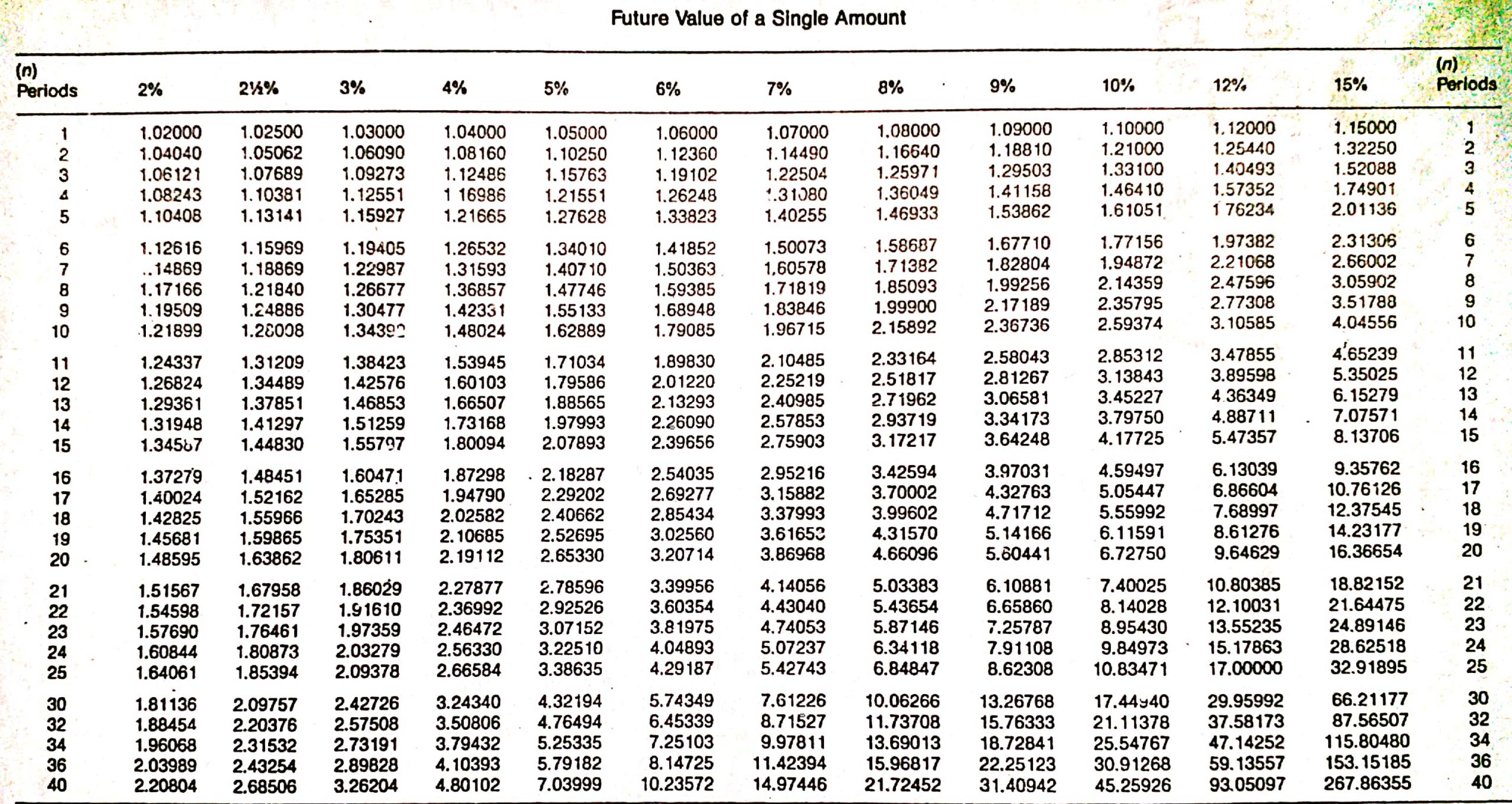
The future value of an annuity is the amount of a series of payments or receipts taken to a future date at a specified interest rate. An annuity is a series of equal payments made at specified intervals. Interest is compounded on each of these payments. Annuities are often called rents because they are like the payment of monthly rentals. Annuity payments can be made at the beginning or end of the specified intervals. If they are made at the beginning of the period, the annuity is called an annuity due; if the payment is made at the end of the period, it is called an ordinary annuity. The examples in this article use ordinary annuities. Therefore, the assumption is made in every article that the payment takes place at the end of the period. Annuities are commonly seen in business and accounting situations. For example, lease payments and mortgages are annuities. Life insurance contracts involving a series of equal payments at equal times are also annuities. In some cases, it is appropriate to calculate the future value of the annuity, and in other cases, it is appropriate to calculate the present value of the annuity. We will first explain how to determine the future value of an annuity. The future value of an annuity is the sum of all the periodic payments plus the interest that has accumulated on them. To demonstrate how to calculate the future value of an annuity, assume that you deposit $1 at the end of each of the next 4 years in a savings account that pays 10% interest compounded annually. The following table shows how these $1 payments will accumulate to $4.6410 at the end of the fourth period (or, in this case, year). The future value of each dollar is determined by compounding interest at 10% for the appropriate number of periods. For example, the $1 deposited at the end of the first period earns interest for 3 periods. It earns interest for only 3 periods because it was deposited at the end of the first period and earns interest until the end of the fourth. Using the factors from the table above, the future value of this first $1 single payment is $1.3310, determined as follows: Future value = Factor x Principal = $1.3310 x $1.00 = $1.3310 The second payment earns interest for 2 periods and accumulates to $1.2100, and the third payment earns interest for only 1 period and accumulates to $1.10. The final payment, made at the end of the fourth year, does not earn any interest because we are determining the future value of the annuity at the end of the fourth period. The total of all payments compounded for the appropriate number of interest periods equals $4.6410 and represents the future value of this ordinary annuity. Fortunately, we do not have to construct a table like this one to determine the future value of an annuity. We can use tables that present the factors necessary to calculate the future value of an annuity of $1, given different periods and interest rates. The table above is such a table. This table is constructed simply by summing the appropriate factors from the compound interest table. For example, the factor for the future value of a $1 annuity at the end of 4 years at 10% compounded annually is $4.6410, which is the amount we determined when we performed the calculation independently by summing the individual factors. With the general formula below, we can solve a variety of problems involving the future value of an annuity. Future value of an annuity = Factor x Annuity payment As long as we know two of the three variables, we can solve for the third. Thus, we can solve for the future value of the annuity, the annuity payment, the interest rate, or the number of periods. Suppose that you deposit $4,000 per year in a savings and loan association at the end of each of the next 8 years. How much will you accumulate if you earn 10% compounded annually? The future value of this annuity is $45,743.56, determined as follows: Future value of an annuity = Factor x Annuity payment = 11.43589 x $4.000 = $45,743.56 Suppose that at end of 15 years, you need to accumulate $100,000 to send your daughter to college. If you can earn 12% at your local savings and loan association, how much do you need to deposit at the end of each of the next 15 years in order to accumulate the $100,000 at the end of the fifteenth year? The annual payment is $2,682.42, as determined in the following: Future value of an annuity = Factor x Annuity payment Annuity payment = Future value of an annuity / Factor = $100,000 / 37.27972 = $2,682.42 In some cases, you may want to determine the interest rate that must be earned on an annuity in order to accumulate a predetermined amount. For example, suppose that you invest $500 per quarter for 10 years and want to accumulate $30,200.99 at the end of the tenth year. What interest rate is required? You need to earn 2% quarterly, or 8% annually, determined as follows: Future value of an annuity = Factor x Annuity payment Factor = Future value of an annuity / Annuity payment = $30,200.99 / $500 = 60.40198 Because the annuity payments are made quarterly, we need to look at the fortieth period (10 years x 4) row until we find the factor (see the table above). In this case, it is in the 2% column. Therefore, the interest rate is 2% quarterly or 8% annually. In some situations, the interest rate is known but the number of periods is missing. You can solve these problems using the same technique we applied to determine the interest rate. When the factor is determined, remember to look down the appropriate interest column to find the factor on the annuity table.What Is the Future Value of an Annuity?
Future Value of an Annuity: Explanation
Examples of Annuities
How to Determine the Future Value of an Annuity
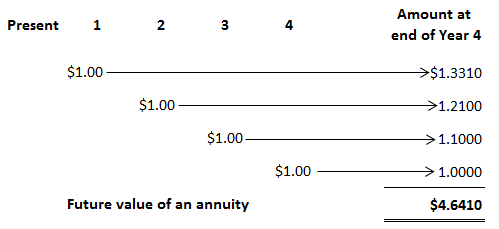
Problems Involving the Future Value of an Annuity
Formula
Determining Future Value
Determining the Annuity Payment
Determining the Interest Rate
Future Value of an Annuity FAQs
The future value of an annuity is the accumulated value of an investment after several periods at a given interest rate.
This means to multiply the factor shown in the table for a given number of periods and interest rate by the periodic investment amount. In other words, find the factor in the table, look at the column for the interest rate you are using, and multiply that factor by your periodic payment.
This formula can be used to solve any number of different problems concerning annuities. If you know two of three variables, you can use this formula to determine the third. Typically, you would be given two of the three variables and asked to solve for the third. However, you can also use this formula if you know the interest rate and period number to calculate your periodic payment. Then, use that payment amount in order to determine how much money will accumulate over a given number of periods.
The annuity payment is a fixed amount of money that you invest over a given number of periods. The amount of money that you receive after the final payment is made at the end of each period is called an annuity payment. The fixed amount you deposit every period to earn interest over time is also called an annuity payment.
This refers to the amount of money you deposit into an account each period. In the examples in this article, a person invested $4,000 per year for 8 years and deposited $500 per quarter for 10 years. The amount you deposit in a given period is called the periodic investment amount.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













