Several authors, including M. Gorden, John Linter, James Walter, and Richardson, are associated with the relevance theory of dividends. According to these authors, a well-reasoned dividend policy can positively influences a firm's position in the stock market. Higher dividends will increase the value of stock, whereas low dividends will have the opposite effect. It is increasingly a reality today that dividends provide an indication of an organization's growing profitability over time. According to James Walter, dividend policy always affects the goodwill of a company. Walter argued that dividend policy reflects the relationship between the firm's return on investment or internal rate of return and the cost of capital or required rate of return. Suppose that r is the internal rate of return and K is the cost of equity capital. Then, for any given company, we have the following cases: Case 1: When r > k Firms with r > k are termed growth firms. Their optimal dividend policy involves ploughing back the company's entire earnings. Thus, the dividend payment ratio would be zero. This would also maximize the market value of the company's shares. Case 2: When r < k Firms with r < k do not offer profitable investment opportunities. For these firms, the optimal dividend policy involves distributing the entire earnings in the form of dividends. Shareholders can use dividends to receive in other channels when they can get a higher rate of dividends. Thus, 100% dividend payout ratio in their case would result in maximizing the value of the equity shares. Case 3: When r = k For firms with r = k, it does not matter whether the firm retains or distributes its earnings. In their case, the share price would not fluctuate with a change in dividend rates. Thus, no optimal dividend policy exists for such firms. (i) The firm undertakes its financing entirely through retained earnings. It does not use external sources of funds such as debts or new equity capital. (ii) The firm's business risk does not change with additional investment. This means that the firm's internal rate of return and cost of capital remain constant. (iii) Initially, earnings per share (EPS) and dividend per share (DPS) remain constant. The choice of values for EPS and DPS varies depending on the model, but any given values are assumed to remain constant. (iv) The firm has a very long life. The market value of a share (P) can be expressed as follows: P = (D + r) (E - D) / KE or P = (D + (r / KE) E-D) / KE where Required: Based on the table shown below concerning companies A, B, and C, calculate the value of each share using Walter's approach when the dividend payment ratio is 50%, 75%, and 25%. In addition, Here, it is better to retain the earnings rather than to distribute them as dividends. As is shown, when the D.P. Ratio is 25%, the share price is $110. Criticisms: Gorden proposed a model along the lines of Walter, suggesting that dividends are relevant and that the dividends of a firm influence its value. The defining feature of Gorden's model is that the value of a dollar in dividend income is greater than the value of a dollar in capital gain. This is due to the uncertainty of the future and the shareholder's discount future dividends at a higher rate. According to Gorden, the market value of a share is equal to the present value of the future stream of dividends. The formula is given as follows: P = E (1 - b) / (Ke - br) or P = D / (Ke - g) where Relevance Theory of Dividends: Definition
Walter's Approach
Assumptions in Models Based on Walter's Approach
Formula for Walter's Approach
Example
A Ltd.
B Ltd.
C Ltd.
r
15%
5%
10%
Ke
10%
10%
10%
e
$8
$8
$8
Solution
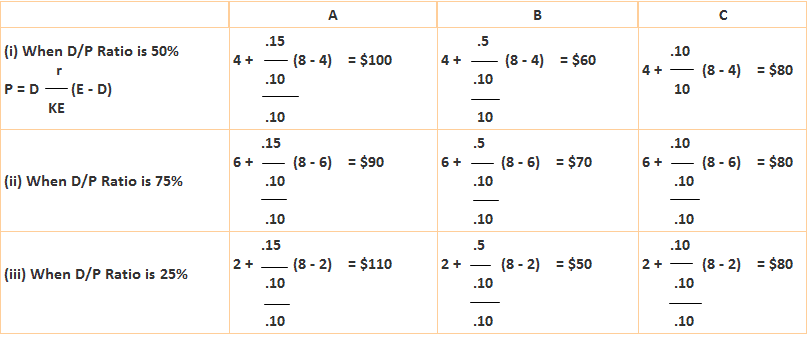
Comment: A Ltd. is a growth firm because its internal rate of return exceeds the cost of capital.
Gorden's Approach
Formula for Gorden’s Approach
Relevance Theory of Dividends FAQs
Relevance theory of dividends states that a well-reasoned dividend policy can positively influences a firm’s position in the stock market. Higher dividends will increase the value of stock, whereas low dividends will have the opposite effect.
According to james walter, dividend policy always affects the goodwill of a company. Walter argued that dividend policy reflects the relationship between the firm’s return on investment or internal rate of return and the cost of capital or required rate of return.
The assumptions of the walter model are:1. The firm undertakes its financing entirely through Retained Earnings. It does not use external sources of funds such as debts or new equity capital.2. The firm’s business risk does not change with additional investment. This means that the firm’s internal rate of return and cost of capital remain constant.3. Initially, earnings per share (eps) and dividend per share (dps) remain constant. The choice of values for eps and dps varies depending on the model, but any given values are assumed to remain constant.4. The firm has a very long life.
The defining feature of gorden’s model is that the value of a dollar in dividend income is greater than the value of a dollar in capital gain. This is due to the uncertainty of the future and the shareholder’s discount future dividends at a higher rate.According to gorden, the market value of a share is equal to the present value of the future stream of dividends.
The formula is given as follows:p = e (1 – b) / (ke – br)orp = d / (ke – g)where:p = share pricee = earnings per shareb = retention ratioke = cost of equity capitalbr = gr = rate of return on investmentd = dividend per share
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.













